Topology Sort(위상정렬)이란 사이클이 없는 방향 그래프에서 노드 순서를 찾는 알고리즘이다.
| 기능 | 특징 | 시간 복잡도 (노드 수 : V, 엣지 수 : E) |
| 노드 간 순서를 결정 | 사이클이 없어야 한다. | O(V+E) |
위상정렬은 항상 유일한 값을 가지며 정렬이 되지 않는다.
또한 사이클이 존재하면 노드 간의 순서를 명확하게 정의할 수 없다. 따라서 위상정렬을 정의할 수없으므로 해당 부분을 염두해야한다.
위상정렬의 원리
1. indegree는 자기 자신을 가리키는 edge의 개수이다.

해당 부분에서 자기 자신을 가리키는 부분을 보면 된다. 인접 리스트를 A라고 하고 다음과 같이 인접 리스트에 기반을 둔 진입 차수 리스트를 만들면 다음과 같다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 2 | 1 | 2 | 1 |
첫 행은 노드를 의미하고 두번째 행은 해당 노드를 가리키는 엣지의 수로 이해하면 된다.
2. indegree (진입 차수) 리스트에서 진입 차수가 0인 노드를 선택한다. [이 부분이 시작]
선택된 노드를 정렬 리스트에서 빼서 저장한다. 이 후 인접 리스트에서 선택된 노드가 가리키는 노드들의 진입 차수를 1씩 뺀다.
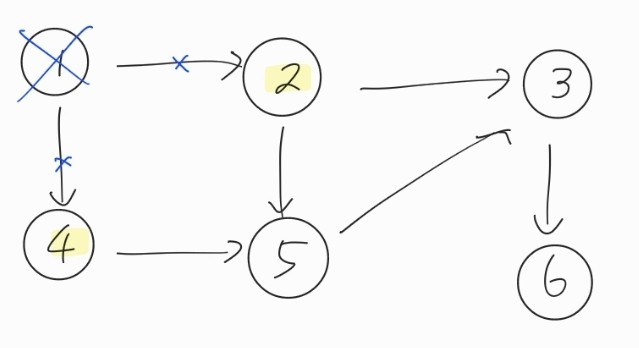
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 -> 0 | 2 | 1 -> 0 | 2 | 1 |
따라서 다음과 같이 자기 자신을 가리키는 엣지가 2, 4 노드에서 하나씩 줄고 위상정렬 리스트에서는 1번 노드만 있었다가 ==> 2, 4 번 노드가 들어온다 (진입 차수리스트가 0인 노드 추가)
:현재 위상 정렬 리스트 = [ 1 ]
일련의 과정을 반복적으로 수행하여 다음 2번 노드를 끊고 본다면 진입 차수 리스트는 다음과 같게 된다
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 2 -> 1 | 0 | 2 -> 1 | 1 |
: 현재 위상 정렬 리스트 = [ 1, 2 ]
* 만약 이어서 4번 노드를 뺄 경우
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 | 0 | 1 -> 0 | 1 |
: 현재 위상 정렬 리스트 = [ 1, 2, 4 ]
이후 다음에 뺄 진입 차수 리스트는 0의 값을 가진 5번 노드가 된다
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 -> 0 | 0 | 0 | 1 |
: 현재 위상 정렬 리스트 = [ 1, 2, 4, 5]
따라서 최종 적인 결과는 3번 노드를 뺴고 이어서 6번 노드까지 빼는 것으로 마무리가 된다
위상정렬의 특징
위상 정렬은 사이클이 없는 방향 그래프 (Direct Acyclic Graph)에서만 수행이 가능하다
위상 정렬에는 답이 unique 하지 않는다. 한 단계에서 queue에 새롭게 들어가는 원소가 2개 이상인 경우가 있다면 여러가지 답이 존재할 수 있다는 의미이다.
모든 원소를 방문하기 전에 queue가 빈다면 사이클이 존재한다.
==> 사이클에 포함된 원소 중 해당되는 어떤 원소도 queue에 들어가지 못하게 된다.
'알고리즘 공부' 카테고리의 다른 글
| Union , Find (0) | 2024.01.09 |
|---|---|
| [알고리즘] Heap sort (힙정렬) (2) | 2024.01.05 |
| Dijkstra Algorithm (다익스트라 알고리즘) (0) | 2023.03.03 |
| Greedy Algorithm (1931 : 회의실 배정) (0) | 2023.03.02 |
| 자주하는 실수 정리 (0) | 2023.02.01 |



